归并排序

归并排序建立在归并操作之上, 它采取分而治之的思想, 将数组拆分为两个子数组, 分别排序, 最后才将两个子数组合并; 拆分的两个子数组, 再继续递归拆分为更小的子数组, 进而分别排序, 直到数组长度为 1, 直接返回该数组为止.

归并排序的另一个优点是非常适合多线程，因为每个被划分出的一半都可以单独排序。另一种常见的减少归并排序运行时间的方法是在到达相对较小的子数组时（大约 7 个元素）使用插入排序。这是因为插入排序在处理小型或几乎排好序的数组时表现非常好。

• 归并排序可通过两种方式实现

  1. 自上而下的递归
  2. 自下而上的迭代

稳定性

稳定

归并排序严格按照从左往右(或从右往左)的顺序去合并子数组, 它并不会改变相同元素之间的相对顺序, 因此它也是一种稳定的排序算法.

演示图

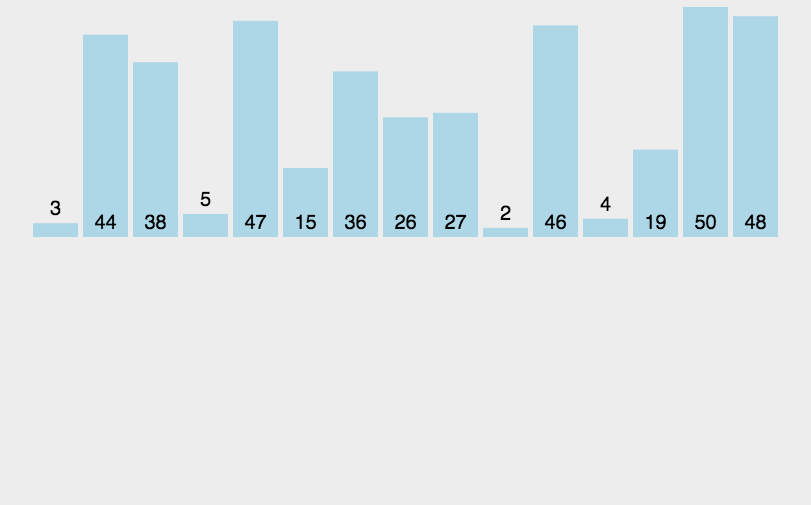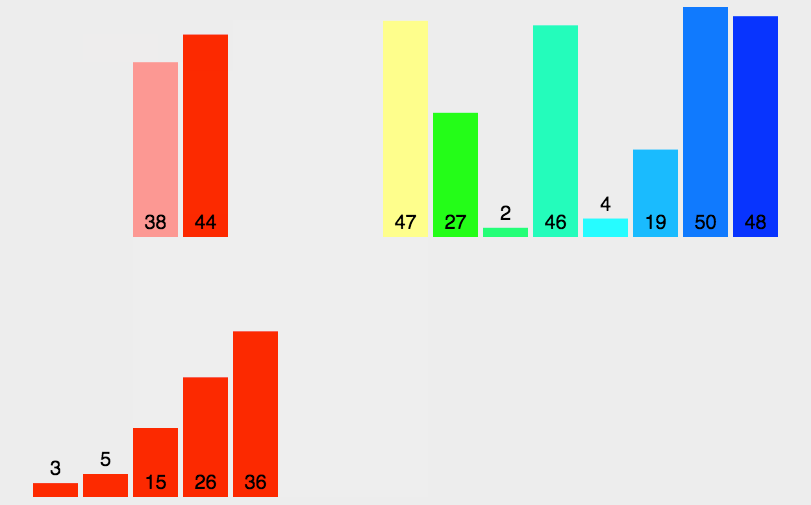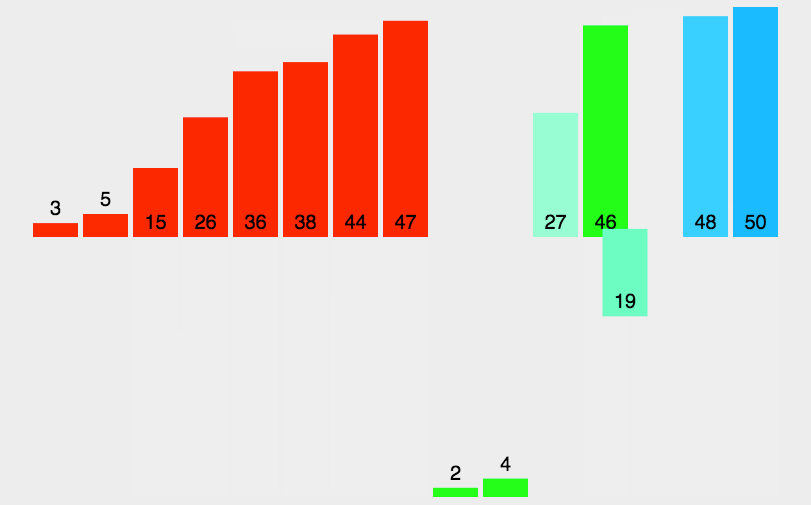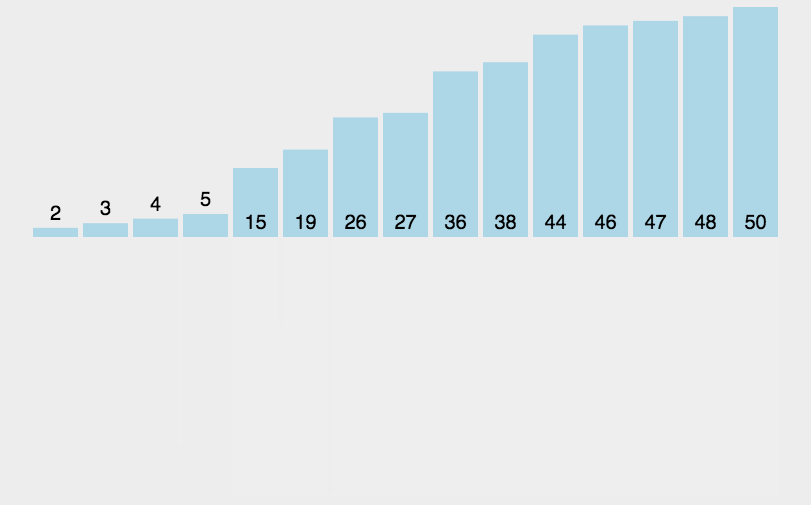
代码实现

• 1. 递归

function mergeSort(array) {
  const half = array.length / 2
  
  if(array.length < 2){
    return array 
  }
  
  const left = array.splice(0, half)
  return merge(mergeSort(left),mergeSort(array))
}
function merge(left, right) {
    let arr = []
    // 如果任何一个数组为空，就退出循环
    while (left.length && right.length) {
        // 从左右子数组的最小元素中选择较小的元素
        if (left[0] < right[0]) {
            arr.push(left.shift())  
        } else {
            arr.push(right.shift()) 
        }
    }
    
    // 连接剩余的元素，防止没有把两个数组遍历完整
    return [ ...arr, ...left, ...right ]
}