树概览

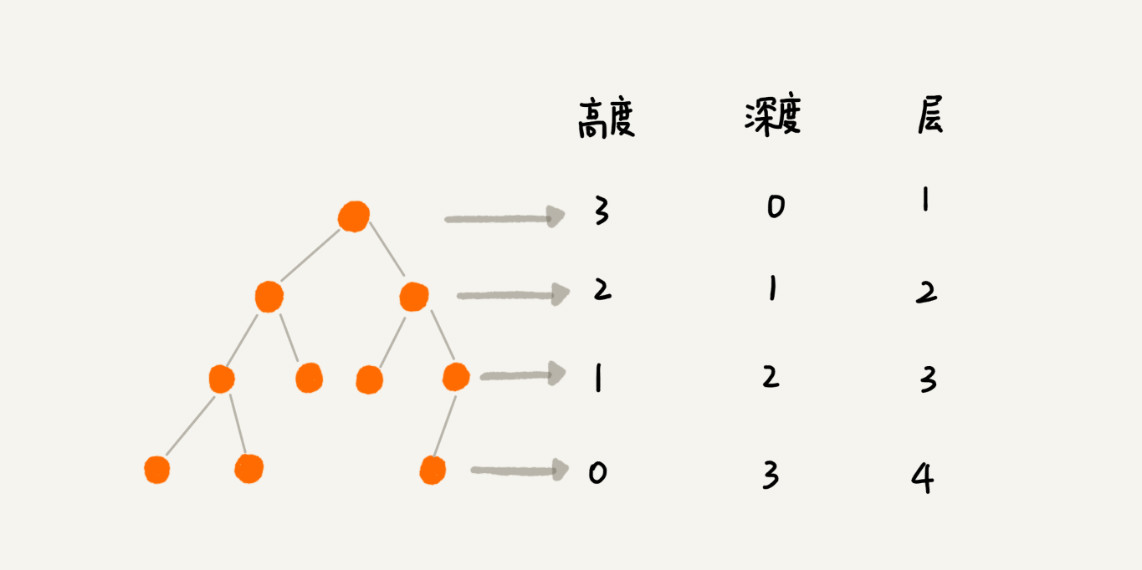
• 树的高度

从下往上数的，等于根节点的高度（0，1，2，3）

• 节点的深度

是根节点到这个节点所经历的边的个数

• 节点的高度

是该节点到叶子节点的最长路径（边数）

• demo 图

  

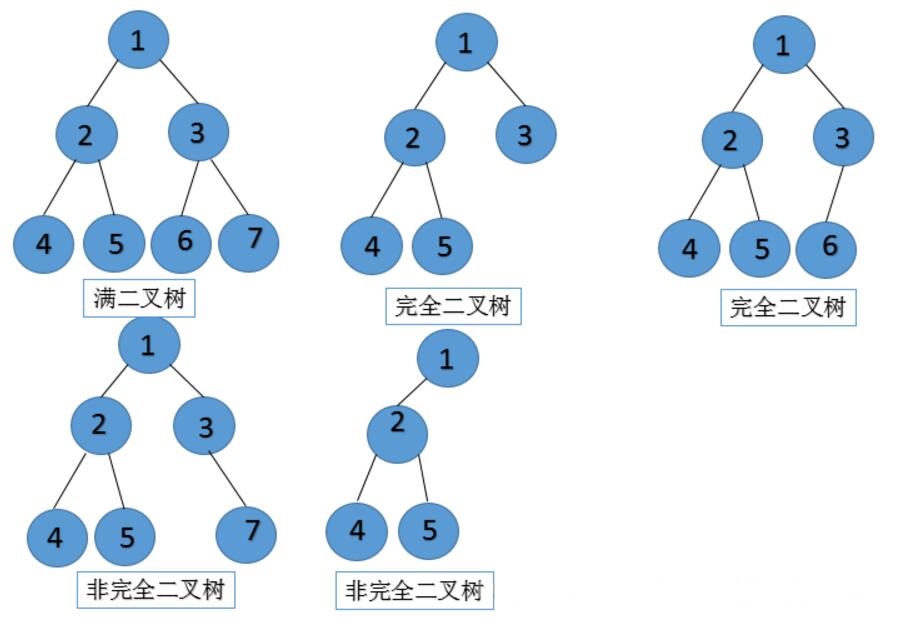
• 完全二叉树

深度为 h，除第 h 层外，其它各层 (1 ～ h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边

满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树

• 满二叉树

一颗深度为 h 且有 2^h-1个结点的二叉树

• 平衡二叉树（AVL Tree）

二叉树中，每一个节点的左右子树的高度相差不能大于 1，称为平衡二叉树

代码表示二叉树

1. 链式存储法

二叉树的存储很简单，在二叉树中，我们看到每个节点都包含三部分：

• 当前节点的 val
• 左子节点 left
• 右子节点 right

所以我们可以将每个节点定义为：

function Node(val) {
  // 保存当前节点 key 值
  this.val = val;
  // 指向左子节点
  this.left = null;
  // 指向右子节点
  this.right = null;
}

一棵二叉树可以由根节点通过左右指针连接起来形成一个树。

function BinaryTree() {
  let Node = function(val) {
    this.val = val;
    this.left = null;
    this.right = null;
  };
  let root = null;
}

数组存储法（适用于完全二叉树）

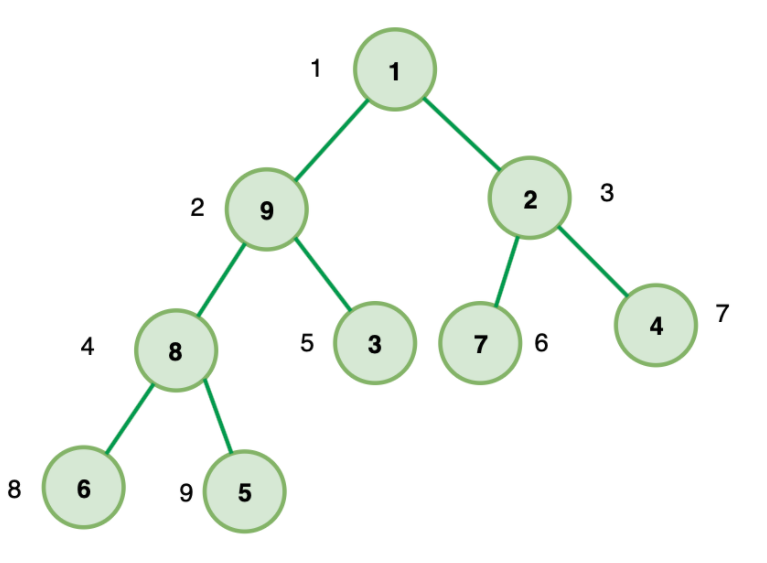
如果我们把根节点存放在位置 i=1 的位置，则它的左子节点位置为 2i = 2 ，右子节点位置为 2i+1 = 3 。

如果我们选取 B 节点 i=2 ，则它父节点为 i/2 = 1 ，左子节点 2i=4 ，右子节点 2i+1=5 。

以此类推，我们发现所有的节点都满足这三种关系：

• 位置为 i 的节点，它的父节点位置为 i/2
• 它的左子节点 2i
• 它的右子节点 2i+1

因此，如果我们把完全二叉树存储在数组里（从下标为 1 开始存储），我们完全可以通过下标找到任意节点的父子节点。从而完整的构建出这个完全二叉树。这就是数组存储法。

数组存储法相对于链式存储法不需要为每个节点创建它的左右指针，更为节省内存。

二叉树的遍历

深度优先遍历(DFS)

1. 前序遍历：访问根结点->遍历左子树->遍历右子树

// 递归实现
var preorderTraversal = function(root, array = []) {
  if (root) {
    array.push(root.val);
    preorderTraversal(root.left, array);
    preorderTraversal(root.right, array);
  }
  return array;
};

// 非递归实现
var preorderTraversal = function(root) {
  const result = [];
  const stack = [];
  let current = root;
  while (current || stack.length > 0) {
    while (current) {
      result.push(current.val);
      stack.push(current);
      current = current.left;
    }
    current = stack.pop();
    current = current.right;
  }
  return result;
};

2. 中序遍历：遍历左子树->访问根结点->遍历右子树

// 递归实现
var inorderTraversal = function(root, array = []) {
  if (root) {
    inorderTraversal(root.left, array);
    array.push(root.val);
    inorderTraversal(root.right, array);
  }
  return array;
};

// 非递归实现
var inorderTraversal = function(root) {
  const result = [];
  const stack = [];
  let current = root;
  while (current || stack.length > 0) {
    while (current) {
      stack.push(current);
      current = current.left;
    }
    current = stack.pop();
    result.push(current.val);
    current = current.right;
  }
  return result;
};

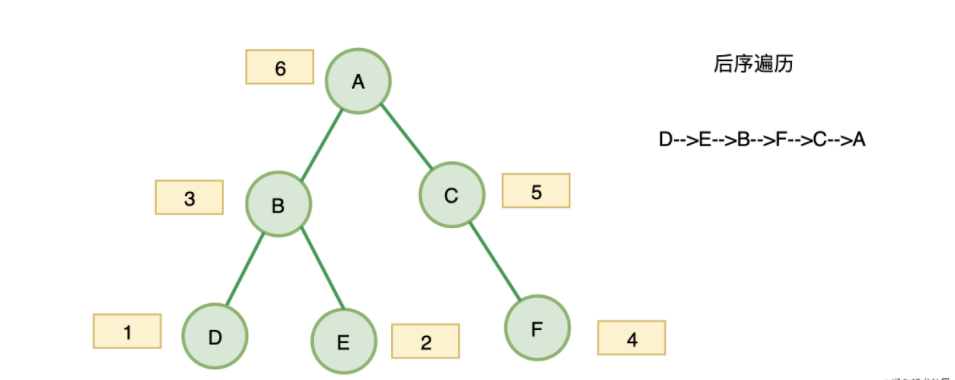
3. 后序遍历：遍历左子树->遍历右子树->访问根结点

// 递归实现
var postorderTraversal = function(root, array = []) {
  if (root) {
    postorderTraversal(root.left, array);
    postorderTraversal(root.right, array);
    array.push(root.val);
  }
  return array;
};

// 非递归实现：我们需要先遍历右子树，再遍历左子树
var postorderTraversal = function(root) {
  // 初始化数据
  const result = [];
  const stack = [];
  while (root || stack.length) {
    while (root) {
      stack.push(root);
      result.unshift(root.val); // 添加到数组开头
      root = root.right;
    }
    root = stack.pop();
    root = root.left;
  }
  return result;
};

所谓前、中、后，不过是根的顺序，即也可以称为先根遍历、中根遍历、后根遍历

广度优先遍历(BFS)

层序遍历：从上往下一层一层遍历，每层按照从左往右遍历

1. 递归实现

广度优先搜索：有一个队列，维护当前深度变量，保证入队列的时候左子节点在右子节点前面

var levelOrder = function(root) {
  const res = [];
  function traversal(root, depth) {
    if (root !== null) {
      // 如果这一层级没有的情况下，初始化为空数组
      if (!res[depth]) res[depth] = [];
      res[depth].push(root.val);
      // 保证左子节点在右子节点前面就行，这样入队列的情况下也能保持左右顺序
      traversal(root.left, depth + 1);
      traversal(root.right, depth + 1);
    }
  }
  traversal(root, 0);
  return res;
};

2. 迭代实现

var levelOrder = function(root) {
  /* 非递归的实现方式 */
  let res = [];
  if (root == null) return res;
  let queue = [root];
  // while 循环控制从上向下一层层遍历
  while (queue.length) {
    let size = queue.length;
    // 记录这一层的节点值
    let level = [];
    // for 循环控制每一层从左向右遍历
    for (let i = 0; i < size; i++) {
      let cur = queue.shift();
      level.push(cur.val);
      if (cur.left != null) queue.push(cur.left);
      if (cur.right != null) queue.push(cur.right);
    }
    res.push(level);
  }
  return res;
};

深度优先遍历(DFS)和广度优先遍历(BFS)区别

1. 二叉树的深度优先遍历的非递归的通用做法是采用栈，广度优先遍历的非递归的通用做法是采用队列。

2. 深度优先遍历：对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。要特别注意的是，二叉树的深度优先遍历比较特殊，可以细分为先序遍历、中序遍历、后序遍历。具体说明如下：

   先序遍历：对任一子树，先访问根，然后遍历其左子树，最后遍历其右子树。

   中序遍历：对任一子树，先遍历其左子树，然后访问根，最后遍历其右子树。

   后序遍历：对任一子树，先遍历其左子树，然后遍历其右子树，最后访问根。

广度优先遍历：又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止。

3. 深度优先搜素算法：不全部保留结点，占用空间少；有回溯操作(即有入栈、出栈操作)，运行速度慢。

广度优先搜索算法：保留全部结点，占用空间大； 无回溯操作(即无入栈、出栈操作)，运行速度快。

通常 深度优先搜索法不全部保留结点，扩展完的结点从数据库中弹出删去，这样，一般在数据库中存储的结点数就是深度值，因此它占用空间较少。

所以，当搜索树的结点较多，用其它方法易产生内存溢出时，深度优先搜索不失为一种有效的求解方法。

广度优先搜索算法，一般需存储产生的所有结点，占用的存储空间要比深度优先搜索大得多，因此，程序设计中，必须考虑溢出和节省内存空间的问题。

但广度优先搜索法一般无回溯操作，即入栈和出栈的操作，所以运行速度比深度优先搜索要快些

实例题-四种遍历结果

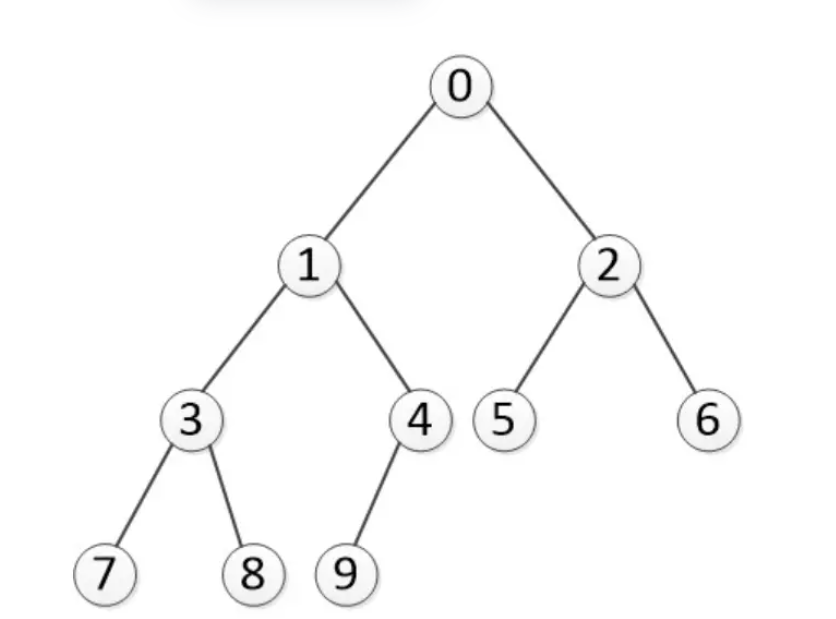
前序遍历结果：0137849256

后续遍历结果：7839415620

中序遍历结果：7381940526

层序遍历结果：0123456789

---

---

参考：前端进阶算法 7：小白都可以看懂的树与二叉树 (opens new window)