//先将交换元素部分抽象出来
function swap(i, j, array) {
  var temp = array[j];
  array[j] = array[i];
  array[i] = temp;
}

冒泡排序简介

稳定性

由于冒泡排序只在相邻元素大小不符合要求时才调换他们的位置, 它并不改变相同元素之间的相对顺序, 因此它是稳定的排序算法.

流程：

1. 从第一个元素开始，比较每两个相邻元素，如果前者大，就交换位置

2. 每次遍历结束，能够找到该次遍历过的元素中的最大值

3. 如果还有没排序过的元素，继续步骤 1

演示图：

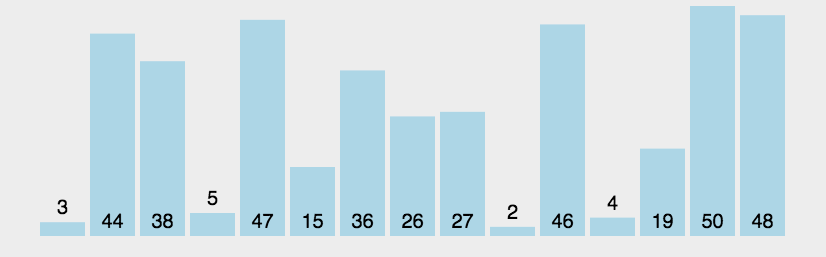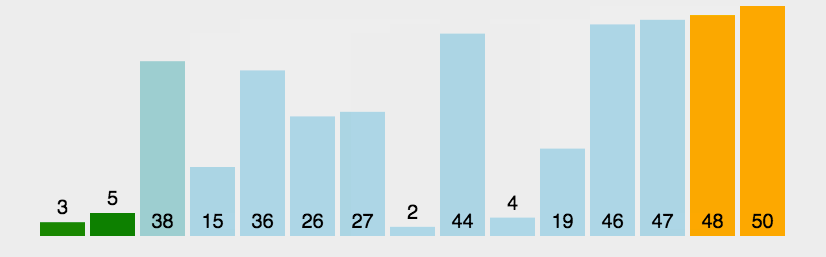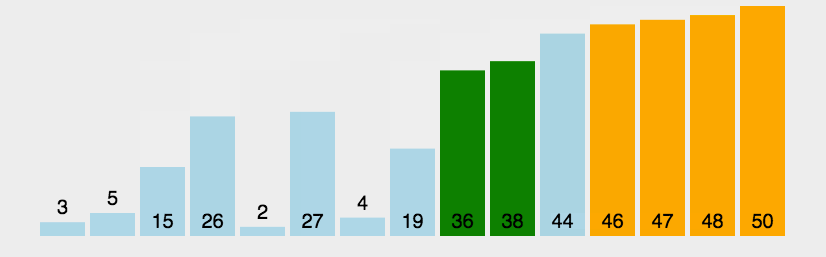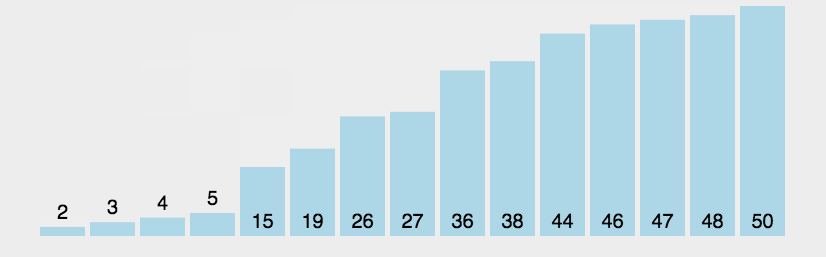
冒泡排序代码实现

最简单的冒泡排序

function bubbleSort(array) {
  for (let i = 0; i < array.length; i++) {
    for (let j = 0; j < array.length - i - 1; j++) {
      if (array[j] > array[j + 1]) {
        swap(j, j + 1, array);
      }
    }
  }
  return array;
}

优化 1：检查某次内层遍历是否发生交换

检查某次内层遍历是否发生交换，如果没有发生交换，说明已经排序完成，就算外层循环还没有执行完 length - 1 次也可以直接 break。

function bubbleSort(array) {
  var length = array.length,
    isSwap;
  for (var i = 0; i < length; i++) {
    //正序
    isSwap = false;
    for (var j = 0; j < length - 1 - i; j++) {
      //正序
      array[j] > array[j + 1] && (isSwap = true) && swap(j, j + 1, array);
    }
    if (!isSwap) break;
  }
  return array;
}

优化 2：记录内层遍历最后一次发生交换的位置

记录内层遍历最后一次发生交换的位置，下一次外层遍历只需要到这个位置就可以了。

那么外层遍历就不能用 for 了，因为每次遍历的结束位置可能会发生改变。

function bubbleSort2(arr) {
  // 遍历结束位置的初始值为数组尾，并逐渐向数组头部逼近
  let high = arr.length - 1;
  while (high > 0) {
    // 本次内层遍历发生交换的位置的初始值
    let position = 0;
    for (let j = 0; j < high; j++) {
      if (arr[j] > arr[j + 1]) {
        swap(j, j + 1, arr);
        // 如果发生了交换，更新 position
        position = j;
      }
    }
    // 下次遍历只需要到 position 的位置即可
    high = position;
  }
  return arr;
}

优化 3：双向冒泡排序

双向遍历，每次循环能找到一个最大值和一个最小值。

前后各设置一个索引，向中间的未排序部分逼近。

function bothwayBubbleSort(array) {
  let left = 0,
    right = array.length - 1;
  for (let i = 0; i < array.length; i++) {
    if (left >= right) {
      // 左侧大于等于右侧，意味着左侧大于等于一半的length，说明已经完成整个排序了
      break;
    }
    let isSwap = false;
    if (i % 2 === 0) {
      // 通过奇偶来区分从左向右，还是从右向左
      for (let j = left; j < right; j++) {
        if (array[j] > array[j + 1]) {
          swap(j, j + 1, array);
          isSwap = true;
        }
      }
      right--; // 从左向右排序，最大的放在最右边，则最后边在下一轮不用参与排序，right --
    } else {
      for (let j = right; j > left; j--) {
        if (array[j - 1] > array[j]) {
          swap(j - 1, j, array);
          isSwap = true;
        }
      }
      left++; // 从右向左排序，最小的放在最左边，最左边最小在下一轮不用参与排序，left ++
    }
    if (!isSwap) {
      // 如果一轮里数据都没有变化，则说明排序完成，可终止排序
      break;
    }
  }
}