希尔排序

希尔排序也称缩小增量排序, 它是直接插入排序的另外一个升级版, 实质就是分组插入排序. 希尔排序以其设计者希尔(Donald Shell)的名字命名, 并于 1959 年公布.

步骤

1. 将数组拆分为若干个子分组, 每个分组由相距一定"增量"的元素组成. 比方说将[0,1,2,3,4,5,6,7,8,9,10]的数组拆分为"增量"为 5 的分组, 那么子分组分别为 [0,5], [1,6], [2,7], [3,8], [4,9] 和 [5,10].

2. 然后对每个子分组应用直接插入排序.

3. 逐步减小"增量", 重复步骤 1,2.

4. 直至"增量"为 1, 这是最后一个排序, 此时的排序, 也就是对全数组进行直接插入排序.

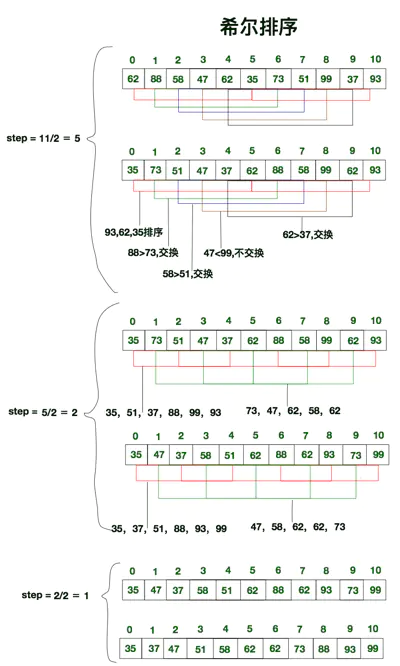
可见, 希尔排序实际上就是不断的进行直接插入排序, 分组是为了先将局部元素有序化. 因为直接插入排序在元素基本有序的状态下, 效率非常高. 而希尔排序呢, 通过先分组后排序的方式, 制造了直接插入排序高效运行的场景. 因此希尔排序效率更高. 我们试着抽象出共同点, 便不难发现上述希尔排序的第四步就是一次直接插入排序, 而希尔排序原本就是从"增量"为 n 开始, 直至"增量"为 1, 循环应用直接插入排序的一种封装. 因此直接插入排序就可以看做是步长为 1 的希尔排序. 为此我们先来封装下直接插入排序.

//形参增加步数gap(实际上就相当于gap替换了原来的数字1)
function directInsertionSort(array, gap) {
  gap = gap == undefined ? 1 : gap; //默认从下标为1的元素开始遍历
  var length = array.length,
    index,
    current;
  for (var i = gap; i < length; i++) {
    index = i - gap; //待比较元素的下标
    current = array[i]; //当前元素
    while (index >= 0 && array[index] > current) {
      //前置条件之一:待比较元素比当前元素大
      array[index + gap] = array[index]; //将待比较元素后移gap位
      index -= gap; //游标前移gap位
    }
    if (index + gap != i) {
      //避免同一个元素赋值给自身
      array[index + gap] = current; //将当前元素插入预留空位
    }
  }
  return array;
}

function shellSort(array) {
  var length = array.length,
    gap = length >> 1,
    current,
    i,
    j;
  while (gap > 0) {
    directInsertionSort(array, gap); //按指定步长进行直接插入排序
    gap = gap >> 1;
  }
  return array;
}

对比上述直接插入排序和折半插入排序, 数组元素的移动次数由 14 次减少为 7 次. 通过拆分原数组为粒度更小的子数组, 希尔排序进一步提高了排序的效率. 不仅如此, 以上步长设置为了 {N/2, (N/2)/2, ..., 1}. 该序列即希尔增量, 其它的增量序列 还有 Hibbard：{1, 3, ..., 2^k-1}. 通过合理调节步长, 还能进一步提升排序效率. 实际上已知的最好步长序列是由 Sedgewick 提出的(1, 5, 19, 41, 109,…). 该序列中的项或者是 94^i - 92^i + 1 或者是 4^i - 3*2^i + 1.

我们知道, 单次直接插入排序是稳定的, 它不会改变相同元素之间的相对顺序, 但在多次不同的插入排序过程中, 相同的元素可能在各自的插入排序中移动, 可能导致相同元素相对顺序发生变化. 因此, 希尔排序并不稳定.